Acción del viento según CTE DB-SE-AE 2009
Para empezar con algo sencillo, este código calculará la presión estática del viento según el Documento Básico SE-AE, edición de abril 2009, del Código Técnico Estructural.
Las tablas de valores iniciales se obtendrán del apartado 3.3 Viento y del Anejo D. Acción del viento. Estos valores se introduciran en diversos DataFrames de pandas. Se operará con ellos para obtener las tablas de valores de un caso particular.
Librerías
Primero se importan las librerías necesarias para el cálculo.
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
from math import ceil, log
Datos iniciales
Presión dinámica
Los valores de la presión dinámica están ligados a la velocidad básica del viento y a las zonas en las que se divide el territorio nacional.
El apartado D.1 y la figura D.1 dan los valores necesarios.
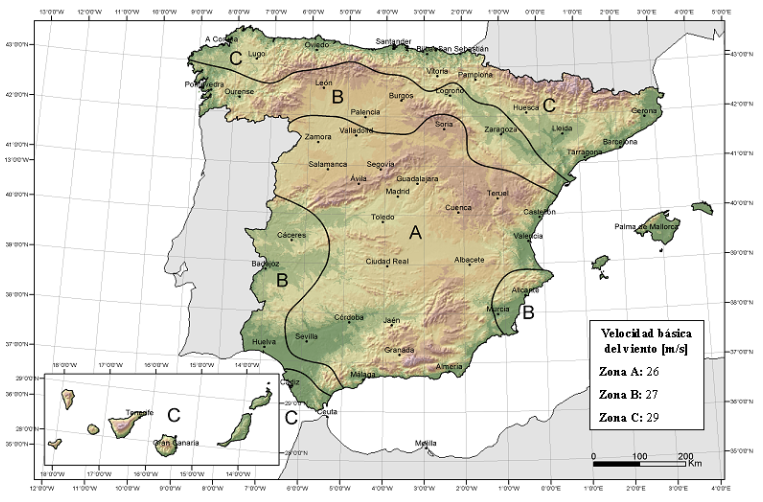
d_presion_dinamica = {
'zonas': ['A', 'B', 'C'],
'velocidad_básica': [26, 27, 28],
'presion_dinámica': [0.42, 0.45, 0.52]
}
df_presion_dinamica = pd.DataFrame.from_dict(d_presion_dinamica)
df_presion_dinamica
| zonas | velocidad_básica | presion_dinámica | |
|---|---|---|---|
| 0 | A | 26 | 0.42 |
| 1 | B | 27 | 0.45 |
| 2 | C | 28 | 0.52 |
Donde:
- zonas: zonas para el valor básico de la velocidad del viento según la figura D.1.
- velocidad_básica: velocidad básica del viento según la figura D.1 en \(m/s\).
- presion_dinámica: valor básico de la presión dinámica en \(kN/m^2\).
Periodo de retorno
Según D.1 (5) los valores de la presión dinámica pueden modificarse según con un coeficiente según el periodo de retorno considerado. Este periodo de retorno es el tiempo igual al periodo de servicio con el que se proyecta la estructura.

d_periodo_retorno = {
'periodo_retorno': [1, 2, 5, 10, 20, 50, 200],
'coeficiente_corrector': [0.41, 0.78, 0.85, 0.90, 0.95, 1.00, 1.08]
}
df_periodo_retorno = pd.DataFrame.from_dict(d_periodo_retorno)
df_periodo_retorno
| periodo_retorno | coeficiente_corrector | |
|---|---|---|
| 0 | 1 | 0.41 |
| 1 | 2 | 0.78 |
| 2 | 5 | 0.85 |
| 3 | 10 | 0.90 |
| 4 | 20 | 0.95 |
| 5 | 50 | 1.00 |
| 6 | 200 | 1.08 |
Donde:
- periodo_retorno: periodo de retorno en años según la tabla D.1.
- coeficiente_corrector: coeficiente corrector según el preiodo de retorno.
Coeficiente de exposición
El entorno de la estructura se clasificará según el grado de aspereza. Los coeficientes de exposición se obtienen según la tabla D.2 para unas alturas \(z\) sobre el terreno no mayores de 200 m.

d_coeficientes_entorno = {
'grados': ['I', 'II', 'III', 'IV', 'V'],
'k': [0.156, 0.17, 0.19, 0.22, 0.24],
'L': [0.003, 0.01, 0.05, 0.3, 1.0],
'Z': [1., 1., 2., 5., 10.]
}
df_coeficientes_entorno = pd.DataFrame.from_dict(d_coeficientes_entorno)
df_coeficientes_entorno
| grados | k | L | Z | |
|---|---|---|---|---|
| 0 | I | 0.156 | 0.003 | 1.0 |
| 1 | II | 0.170 | 0.010 | 1.0 |
| 2 | III | 0.190 | 0.050 | 2.0 |
| 3 | IV | 0.220 | 0.300 | 5.0 |
| 4 | V | 0.240 | 1.000 | 10.0 |
Donde:
- grados: grados de aspereza del entorno según la tabla D.2.
- k: parámetro característico de cada tipo de entorno según la tabla D.2.
- L: parámetro característico de cada tipo de entorno según la tabla D.2 en \(m\).
- Z: parámetro característico de cada tipo de entorno según la tabla D.2 en \(m\).
El coeficiente de exposición se define por las expresiones D.2 y D.3
\(c_e = F · (F + 7 · k) \qquad \qquad (D.2)\) \(F = k · \ln(\max(z, Z) / L) \qquad (D.3)\)
Coeficientes de presión exterior e interior
No es objeto de este cálculo obtener los diferentes coeficientes de presion exterior e interior a fin de no complicar el código.
Se tomará por defecto para estos coeficientes el valor de 1,0. En un cálculo detallado se puede aplicar los valores adecuados al resultado final de este cálculo.
cpi = 1.0 # Coeficiente de presión interior.
cpe = 1.0 # Coeficiente de presión exterior.
Presión estática
Presión estática debida a la acción del viento y actuando perpendicularmente a la superficie expuesta.
\[q_e = q_b · c_e · c_p · \text{cc}\]Donde:
- \(q_e\): presión estática en \(kN/m²\).
- \(q_b\): presión dinámica en \(kN/m²\).
- \(c_e\): coeficiente de exposición.
- \(c_p\): coeficiente eólico.
- \(cc\) : coeficiente corrector debido al periodo de retorno.
Caso de estudio
En este caso de estudio se obtendrán los valores correspondientes a la acción del viento de un edificio situado en el puerto de Huelva con un periodo de retorno de 50 años y a intervalos de altura de 1 m.
Presión dinámica
Zona
zona = 'B' # <-- Entrada de datos.
print('Zona:', zona)
Zona: B
Velocidad básica
vb = df_presion_dinamica['velocidad_básica'].loc[
df_presion_dinamica['zonas'] == zona
].values.item()
print('vb =', vb, 'm/s')
vb = 27 m/s
Presión dinámica
qb = df_presion_dinamica['presion_dinámica'].loc[
df_presion_dinamica['zonas'] == zona
].values.item()
print('qb =', qb, 'kN/m²')
qb = 0.45 kN/m²
Periodo de retorno
pr = 50 # años. <-- Entrada de datos.
print('Periodo de retorno de', pr, 'años.')
Perido de retorno de 50 años.
cc = df_periodo_retorno['coeficiente_corrector'].loc[
df_periodo_retorno['periodo_retorno'] == pr
].values.item()
print('Coeficiente corrector =', cc)
Coeficiente corrector = 1.0
Coeficiente de exposición
Grado de aspereza
grado = 'I' # <-- Entrada de datos.
print('Grado de aspereza =', grado)
Grado de aspereza = I
Parámetro \(k\)
k = df_coeficientes_entorno['k'].loc[
df_coeficientes_entorno['grados'] == grado
].values.item()
print('k =', k)
k = 0.156
Parámetro \(L\)
L = df_coeficientes_entorno['L'].loc[
df_coeficientes_entorno['grados'] == grado
].values.item()
print('L =', L, 'm')
L = 0.003 m
Parámetro \(Z\)
Z = df_coeficientes_entorno['Z'].loc[
df_coeficientes_entorno['grados'] == grado
].values.item()
print('Z =', Z, 'm')
Z = 1.0 m
Altura sobre el terreno \(z\) ≤ 200 \(m\)
z = np.arange(start=0, stop=201, step=1)
print('Altura sobre el terreno en los primeros 10 m =', z[:11], 'm')
Altura sobre el terreno en los primeros 10 m = [ 0 1 2 3 4 5 6 7 8 9 10] m
Coeficiente de exposición
max_z = np.array([max(i, Z) for i in z])
F = k * np.log(max_z / L)
ce = F * (F + 7 * k)
print('Coeficiente de exposición en los primeros 30 m cada 5 m =')
print(ce[0:31:5])
Coeficiente de exposición en los primeros 30 m cada 5 m =
[1.81084525 2.60311019 2.98316113 3.21631712 3.38659667 3.52144975
3.63343178]
Presión estática
df = pd.DataFrame()
df['z'] = z
df['v.b'] = vb
df['q.b'] = qb
df['grado'] = grado
df['c.e'] = np.around(ce, decimals=3)
df['c.pi'] = cpi
df['c.pe'] = cpe
df['cc'] = cc
df['q.e'] = np.around(qb * ce * cpi * cpe * cc, decimals=2)
qer = df['q.e'].loc[df['z'] == 10].values.item()
df['r'] = np.around(df['q.e'] / qer, decimals=2)
Esto da un DataFrame con los siguientes valores extremos:
df
| z | v.b | q.b | grado | c.e | c.pi | c.pe | cc | q.e | r | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 27 | 0.45 | I | 1.811 | 1.0 | 1.0 | 1.0 | 0.81 | 0.60 |
| 1 | 1 | 27 | 0.45 | I | 1.811 | 1.0 | 1.0 | 1.0 | 0.81 | 0.60 |
| 2 | 2 | 27 | 0.45 | I | 2.137 | 1.0 | 1.0 | 1.0 | 0.96 | 0.72 |
| 3 | 3 | 27 | 0.45 | I | 2.338 | 1.0 | 1.0 | 1.0 | 1.05 | 0.78 |
| 4 | 4 | 27 | 0.45 | I | 2.486 | 1.0 | 1.0 | 1.0 | 1.12 | 0.84 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 196 | 196 | 27 | 0.45 | I | 4.880 | 1.0 | 1.0 | 1.0 | 2.20 | 1.64 |
| 197 | 197 | 27 | 0.45 | I | 4.884 | 1.0 | 1.0 | 1.0 | 2.20 | 1.64 |
| 198 | 198 | 27 | 0.45 | I | 4.888 | 1.0 | 1.0 | 1.0 | 2.20 | 1.64 |
| 199 | 199 | 27 | 0.45 | I | 4.891 | 1.0 | 1.0 | 1.0 | 2.20 | 1.64 |
| 200 | 200 | 27 | 0.45 | I | 4.895 | 1.0 | 1.0 | 1.0 | 2.20 | 1.64 |
201 rows × 10 columns
Donde:
- \(z\): altura sobre el terreno en \(m\).
- \(q_b\): valor básico de la presión dinámica en \(kN/m²\).
- \(c_e\): coeficiente de exposición.
- \(c_{pi}\): coeficiente de presión interior.
- \(c_{pe}\): coeficiente de presión exterior.
- \(q_e\): presión estática en \(kN/m²\).
- \(r\): relación de presiones estáticas con respecto a \(q_e (z = 10 \text{ m})\).
Además de la presión estática \(q_e\) se ha calculado el ratio \(r\) de las diferentes presiones estáticas tomando como referencia la presión estática a un altura \(z\) de 10 m.
Resultados con unos rangos de valores más acotados
El DataFrame anterior da unos resultados para unas alturas que van desde \(z\) = 0 m a \(z\) = 200 m a intervalos de 1 m. Puede interesar ver los resultados únicamente dentro de un rango más limitado, siendo además más fácil acceder a los valores.
Por ejemplo, puede ser que solo interese conocer los valores hasta una altura máxima de 30 m y a intervalos de 5 m
z_min = 0 # [m] Altura mínima de estudio. <-- Entrada de datos.
z_max = 30 # [m] Altura máxima de estudio. <-- Entrada de datos.
z_paso = 5 # [m] Intervalos <-- Entrada de datos.
df_1 = df.loc[z_min:z_max].where(df['z'] % z_paso == 0).dropna()
df_1
| z | v.b | q.b | grado | c.e | c.pi | c.pe | cc | q.e | r | |
|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0.0 | 27.0 | 0.45 | I | 1.811 | 1.0 | 1.0 | 1.0 | 0.81 | 0.60 |
| 5 | 5.0 | 27.0 | 0.45 | I | 2.603 | 1.0 | 1.0 | 1.0 | 1.17 | 0.87 |
| 10 | 10.0 | 27.0 | 0.45 | I | 2.983 | 1.0 | 1.0 | 1.0 | 1.34 | 1.00 |
| 15 | 15.0 | 27.0 | 0.45 | I | 3.216 | 1.0 | 1.0 | 1.0 | 1.45 | 1.08 |
| 20 | 20.0 | 27.0 | 0.45 | I | 3.387 | 1.0 | 1.0 | 1.0 | 1.52 | 1.13 |
| 25 | 25.0 | 27.0 | 0.45 | I | 3.521 | 1.0 | 1.0 | 1.0 | 1.58 | 1.18 |
| 30 | 30.0 | 27.0 | 0.45 | I | 3.633 | 1.0 | 1.0 | 1.0 | 1.64 | 1.22 |
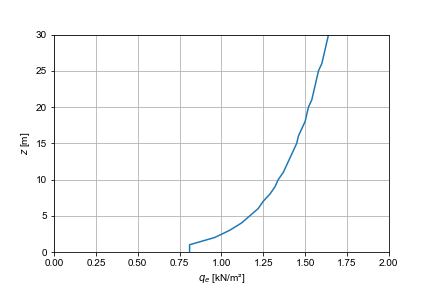
Gráfica
Representación gráfica de los resultados de la presión estática.
x_max = df['q.e'].loc[df['z'] == z_max].values.item()
x_max = ceil(x_max)
xlim=[0, x_max]
ylim=[0, z_max]
df.plot(
kind='line', x='q.e', y='z',
xlim=xlim, ylim=ylim, legend=False, grid=True
)
plt.style.use('seaborn-whitegrid')
plt.xlabel('$q_e$ [kN/m²]')
plt.ylabel('$z$ [m]')
plt.savefig('grafica.png') # Guarda la gráfica como imagen para poder incorporarla a la hoja Excel.
plt.show()
Resultados para una altura determinada
Igualmente puede ocurrir que solo interese ver los resultados para una altura determinada.
Por ejemplo, veamos los resultados para una altura \(z\) = 22 m.
z_i = 22 # [m] Altura z en la posición i. <-- Entrada de datos.
ce = df.loc[df['z'] == z_i, 'c.e'].item()
qe = df.loc[df['z'] == z_i, 'q.e'].item()
print('Zona : {}'.format(zona))
print('Velocidad básica : {} m/s'.format(vb))
print('Presión dinámica : {} kN/m²'.format(qb))
print('Periodo de retorno : {}'.format(pr))
print('Coeficiente corrector : {}'.format(cc))
print('Grado de aspereza : {}'.format(grado))
print('Parámetro k : {}'.format(k))
print('Parámetro L : {}'.format(L))
print('Parámetro Z : {}'.format(Z))
print('Coeficiente de presión interior : {}'.format(cpi))
print('Coeficiente de presión exterior : {}'.format(cpe))
print('Altura sobre el terreno : {} m'.format(z_i))
print('Coeficiente de exposición : {}'.format(ce))
print('Presión estática : {} kN/m²'.format(qe))
Zona : B
Velocidad básica : 27 m/s
Presión dinámica : 0.45 kN/m²
Periodo de retorno : 50
Coeficiente corrector : 1.0
Grado de aspereza : I
Parámetro k : 0.156
Parámetro L : 0.003
Parámetro Z : 1.0
Coeficiente de presión interior : 1.0
Coeficiente de presión exterior : 1.0
Altura sobre el terreno : 22 m
Coeficiente de exposición : 3.444
Presión estática : 1.55 kN/m²
Exportar DataFrame a Excel
Finalmente los datos se pueden exportar a una hoja de cálculo Excel.
libro = 'acción_viento.xlsx' # Nombre del libro de cálculo Excel. <-- Entrada de datos.
hoja = 'CTE DB-SE-AE 2009' # Nombre de la hoja de cálculo Excel. <-- Entrada de datos.
writer = pd.ExcelWriter(libro, engine='xlsxwriter')
df_1.to_excel(writer, sheet_name=hoja)
workbook = writer.book
worksheet = writer.sheets[hoja]
format1 = workbook.add_format()
format1.set_align('center')
worksheet.set_column('B:K', 8, format1)
worksheet.insert_image('M1', 'grafica.png')
writer.save()
Versión
%load_ext version_information
%version_information matplotlib, numpy, pandas
| Software | Version |
|---|---|
| Python | 3.7.6 64bit [MSC v.1916 64 bit (AMD64)] |
| IPython | 7.12.0 |
| OS | Windows 10 10.0.18362 SP0 |
| matplotlib | 3.1.3 |
| numpy | 1.18.1 |
| pandas | 1.0.1 |
| Tue May 19 18:42:44 2020 Hora de verano romance | |


Comentar