Comprobación de miembros sujetos a fatiga según FEM 2131/2132 (1)

Introducción

En el diseño de máquinas de manutención continua como apiladoras, recogedoras, cargadores de barcos, etc. se emplean diversas normas de diseño. Uno de los códigos más reconocidos internacionalmente es FEM 2131/2132 Rules for the Design of Mobile Equipment for Continuous Handling of Bulk Materials. La norma tiene sus orígenes en los años 80 y la última edición es de 1997. Aunque emplea criterios que las nuevas normas ya no contemplan, sigue siendo una norma vigente en este tipo de cálculos.

Excavadora recogedora con rueda de cangilones

Al ser estructuras máquinas móviles, donde las posiciones y estados de carga cambian contínuamente, el cálculo de la fatiga es un punto sensible en el diseño.

En general, es obligatorio comprobar la tensión de fatiga cuando se superan los 250.000 ciclos de carga durante la vida útil de la máquina. En este caso, la resistencia a fatiga de un material depende del grupo de la componente y de la concentración de tensión o efecto de entalladura.

El grupo de la componente depende del número de ciclos de tensión y de la clase del espectro. Normalmente está definido en las especificaciones del proyecto y se clasifica como E1, E2, …, E8. Habitualmente se considera aceptable los grupos E6, E7 y E8. Más información al respecto se puede encontrar en el capítulo de la norma 2-1 Group Classificaction of Mobile Equipment and their Components.

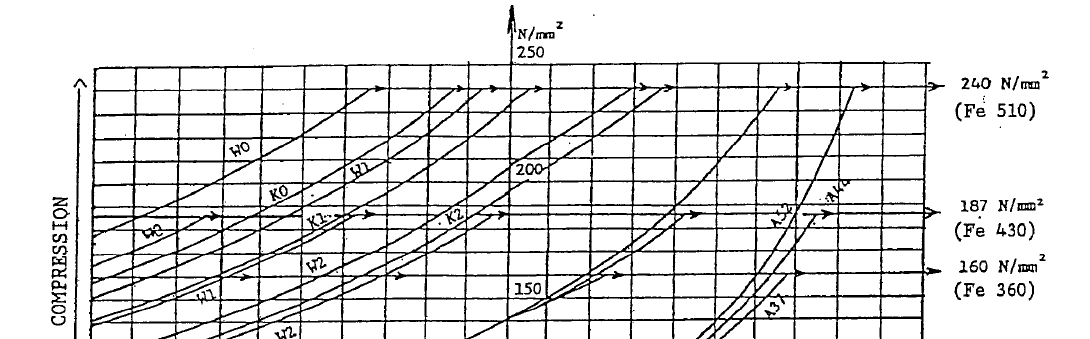
El efecto de entalladura depende del detalle constructivo del punto estudiado. En la tabla T.3-4.5.2.3 se muestran diferentes detalles constructivos con su clasificación.

La tensión máxima \(\sigma_{max}\) no podrá superar la tensión admisible \(\sigma_a\) que depende de la tensión básica \(\sigma_W\) y del ratio \(\kappa\) entre los valores de las tensiones extremas.

La tensión admisible \(\sigma_a\) depende de la tensión crítica que corresponde a un 90 % de probabilidad de supervivencia con un coeficiente de seguridad de 1,33.

\[\sigma_{a \text{ for fatigue}} = \frac{\sigma_{\text{at 90 % survival}}}{1,33} = 0,75 \cdot \sigma_{\text{at 90 % survival}}\]

La determinación de esta tensión admisible es un problema complejo. FEM propone para la comprobación de elementos sometidos a fatiga el método que voy a mostrar en los siguientes posts. Para los siguientes cálculos partiré de un DataFrame de pandas generado aleatoriamente. Las columnas del DataFrame serán:

• bar
• node
• component_group
• notch_effect
• sigma_x_max_[MPa]
• sigma_x_min_[MPa]
• sigma_y_max_[MPa]
• sigma_y_min_[MPa]
• tau_xy_max_[MPa]
• tau_xy_min_[MPa]

Donde:

• Las barras y los nudos son las barras y los nudos del programa de cálculo estructural donde se han obtenido los supuestos datos.
• El grupo de la componente y el efecto de entalladura son los supuestos datos obtenidos de la especificación del proyecto y del detalle constructivo en el punto analizado. El grupo de la componente se ha limitado a E6, E7 y E8, dando algo más de presencia a E8 por ser el más habitual. El efecto de la entalladura se limita a los casos K que son más restrictivos y habitualmente estudiados.
• Las tensiones son las tensiones \(\sigma_x\), \(\sigma_y\) y \(\tau_{xy}\) máximas y mínimas de la barra. Al ser una supuesta estructura formada por barras, las tensiones predominantes \(\sigma\) son en el eje \(x\). La tensión cortante \(\tau_{xy}\) tampoco suele ser de gran magnitud. Si la estructura fuera a base de chapa armada, tal como suelen ser los cuerpos de giro y las infraestructuras de este tipo de máquinas, la tensión \(\sigma_y\) tendría unos valores considerablemente superiores.

Primero creo las listas con los valores aleatorios de las columnas del DataFrame.

import random

random.seed(0)

barras = []
nudos = []
grupo_componente = []
entalladura = []
sigma_x_max = []
sigma_x_min = []
sigma_y_max = []
sigma_y_min = []
tau_xy_max = []
tau_xy_min = []

for i in range(10):
    barras.append(i + 1)
    nudos.append(i + 1)
    grupo_componente.append(random.choice(['E6', 'E7', 'E8', 'E8']))
    entalladura.append(random.choice(['K0', 'K1', 'K2', 'K3', 'K4']))
    sigma_x_max.append(random.randint(-150, 150))
    sigma_y_max.append(random.randint(-5, 5))
    tau_xy_max.append(random.randint(-10, 10))

sigma_x_min = [int(i * random.uniform(-1, 1)) for i in sigma_x_max]
sigma_y_min = [int(i * random.uniform(-1, 1)) for i in sigma_y_max]
tau_xy_min = [int(i * random.uniform(-1, 1)) for i in tau_xy_max]

Con estas listas genero el DataFrame.

df = pd.DataFrame()
df['bar'] = barras
df['node'] = nudos
df['component_group'] = grupo_componente
df['notch_effect'] = entalladura
df['sigma_x_max_[MPa]'] = sigma_x_max
df['sigma_x_min_[MPa]'] = sigma_x_min
df['sigma_y_max_[MPa]'] = sigma_y_max
df['sigma_y_min_[MPa]'] = sigma_y_min
df['tau_xy_max_[MPa]'] = tau_xy_max
df['tau_xy_min_[MPa]'] = tau_xy_min
df

	bar	node	component_group	notch_effect	sigma_x_max_[MPa]	sigma_x_min_[MPa]	sigma_y_max_[MPa]	sigma_y_min_[MPa]	tau_xy_max_[MPa]	tau_xy_min_[MPa]
0	1	1	E8	K3	-130	-59	-1	0	6	0
1	2	2	E8	K3	5	2	2	1	1	0
2	3	3	E7	K4	-79	69	-1	0	-6	4
3	4	4	E6	K4	-22	-18	3	-1	9	5
4	5	5	E7	K2	-100	55	-4	1	0	0
5	6	6	E8	K4	-99	-60	0	0	3	-1
6	7	7	E8	K4	-46	32	3	-1	5	-3
7	8	8	E8	K4	-17	-1	-5	-4	7	4
8	9	9	E6	K0	54	-44	5	-2	10	-9
9	10	10	E6	K4	102	100	0	0	-3	-2

Una vez tengo los datos de las tensiones en los puntos donde se quiere estudiar la fatiga defino las propiedades del acero

En el siguiente post crearé el código para introducir el acero según la nomenclatura ISO o EN 1993 y buscar sus propiedades en una base de datos de materiales.