Comprobación de miembros sujetos a fatiga según FEM 2131/2132 (4)

Tensiones de tracción y compresión

Tensión básica \(\sigma_W\)

Conocidos el grupo de la componente y el efecto de entalladura, el valor de la tensión \(\sigma_W\) se obtiene de la tabla T.3-4.5.1.1.

Valores de la tensión básica sigma_W

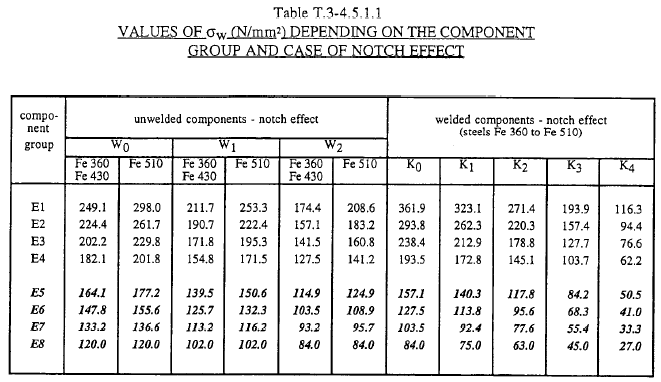
El código FEM no indica ninguna función para obtener los valores de esta tabla, la solución para incorporar estos valores al código ha sido crear una pequeña base de datos.

Defino primero el directorio donde se encuentra la base de datos con los valores \(\sigma_W\) y el nombre de la base de datos

cwd = 'midirectorio/SQLite/fem'
db = 'sigmaW.db'

Creo la conexión y asigno la tabla de la base de datos a un DataFrame:

con = sqlite3.connect(cwd + '/' + db)
df_sW = pd.read_sql(
    'SELECT * FROM ' + steel_db + ';', conn
    )
df_sW

	component_group	W0	W1	W2	K0	K1	K2	K3	K4
0	E1	298.0	253.3	208.6	361.9	323.1	271.4	193.9	116.3
1	E2	261.7	222.4	183.2	293.8	262.3	220.3	157.4	94.4
2	E3	229.8	195.3	160.8	238.4	212.9	178.8	127.7	76.6
3	E4	201.8	171.5	141.2	193.5	172.8	145.1	103.7	62.2
4	E5	177.2	150.6	124.9	157.1	140.3	117.8	84.2	50.5
5	E6	155.6	132.3	108.9	127.5	113.8	95.6	68.3	41.0
6	E7	136.6	116.2	95.7	103.5	92.4	77.6	55.4	33.3
7	E8	120.0	102.0	84.0	84.0	75.0	63.0	45.0	27.0

El siguiente paso consiste en crear una nueva columna en el DataFrame con los valores de la tensión básica \(\sigma_W\) correspondiente:

df = df.join(
    df_sW.set_index('component_group').stack().rename('sigma_W_[MPa]'),
    on=['component_group','notch_effect']
    )
cols = [
    'bar', 'node', 'component_group', 'notch_effect', 'sigma_W_[MPa]'
    ]
df[cols]

	bar	node	component_group	notch_effect	sigma_W_[MPa]
0	1	1	E8	K3	45.0
1	2	2	E8	K3	45.0
2	3	3	E7	K4	33.3
3	4	4	E6	K4	41.0
4	5	5	E7	K2	77.6
5	6	6	E8	K4	27.0
6	7	7	E8	K4	27.0
7	8	8	E8	K4	27.0
8	9	9	E6	K0	127.5
9	10	10	E6	K4	41.0

Tensión admisible a tracción \(\sigma_t\) y compresión \(\sigma_c\) para la fatiga

Conocidas las tensiones básicas \(\sigma_W\) que se aplican en cada punto del estudio queda por definir las tensiones admisibles a tracción \(\sigma_t\) y compresión \(\sigma_c\).

Primero veamos que dice el código FEM (3-4.5.1.1):

• Si \(\kappa \leq 0\)

  para tracción:

  \[\sigma_t = \sigma_W · \frac{5}{3 – 2 · \kappa} \leq 0,66 · \sigma_E \tag*{(1)}\]

  para compresión:

  \[\sigma_c = \sigma_W · \frac{2}{1 - \kappa} \tag*{(2)}\]

• Si \(\kappa > 0\)

  para tracción:

  \[\sigma_t = \frac{\sigma_O}{1 - \left(1 - \dfrac{\sigma_O}{\sigma_{+1}}\right) · \kappa} \leq 0,66 · \sigma_E \tag*{(3)}\]

  para compresión:

  \[\sigma_c = 1,2 · \sigma_t \tag*{(4)}\]

Donde

\(\sigma_0\) = tensión de tracción para \(\kappa\) = 0; se da en la fórmula (1), esto es:

\[\sigma_0 = 1,66 · \sigma_W\]

\(\sigma_{+1}\) = tensión de tracción para \(\kappa\) = +1, esto es, la tensión última \(\sigma_R\) dividida por el coeficiente de seguridad 1,33:

\[\sigma_{+1} = 0,75 · \sigma_R\]

\(\sigma_t\) está limitada en todo caso a \(0,66 · \sigma_E\)

Para traducir esto a un código de Python emplearé tres clases diferentes:

• Una primera clase llamada DataFrame donde obtendré los valores básicos para calcular las tensiones admisibles.
• Una segunda clase Formulae contendrá todo el formulario necesario para el cálculo (sin entrar en ningún tipo de consideración).
• Y en una tercera clase PermissibleSigma obtendré las tensiones admisibles según las diferentes condiciones.

Esta organización del código dividida en tres abstracciones diferentes me permite tener organizado el código de tal manera que si el código tuviera un error resultaría más fácil de detectarlo y acotarlo. Por otra parte, si los criterios de la norma cambiaran, o bien yo mismo decidiera hacer una nueva revisión del código, podría reescribir únicamente las partes afectadas sin verse afectadas el resto. Por ejemplo, si una nueva edición del código de diseño modificara las fórmulas, pero mantuviera los criterios de las condiciones de su aplicación, tendría que modificar los métodos de la clase Formulae, dejando las clases DataFrame y PermissibleStress inalteradas.

Mi primera clase DataFrame:

class DataFrame:
    """
    Pandas DataFrame with the data for the calculation of the 
    stresses for fatigue.
    """
    
    def __init__(self, df):
        """
        Asumes df is the pandas DataFrame with the data for the 
        calculation of the stresses for fatigue, get the values 
        of the columns.
        
        Parameters
        ----------
        df : pandas DataFrame ; data for the calculation of the 
        stresses for fatigue.
        """
        
        self.df = df

La única variable de instancia de la clase DataFrame es df. df se supone que no es otra más que el DataFrame con los datos del estudio de la fatiga.

Los siguientes métodos de la clase DataFrame son los getters de las variables necesarias para el cálculo.

    def get_sigma_W(self):
        """Basic stress [MPa]."""
        
        return self.df['sigma_W_[MPa]'].copy()
    
    def get_k_sx(self):
        """Ratio between the extreme stresses sigma_x."""
        
        return self.df['k_sx'].copy()
    
    def get_k_sy(self):
        """Ratio between the extreme stresses sigma_y."""
        
        return self.df['k_sy'].copy()

La segunda clase Formulae es algo más interesante. Hereda de la clase DataFrame los diferentes atributos para operar, además inicializa las variables de instancia del límite elástico \(\sigma_E\) y la tensión de rotura \(\sigma_R\).

class Formulae(DataFrame):
    """
    Formulae for the permissible stresses for fatigue with tensile 
    and comprensive loads according to FEM 2131/2132.
    """
    
    def __init__(self, df, sigma_E, sigma_R):
        """
        Asumes df, sigma_E and sigma_R the data for the calculation 
        of the stresses for fatigue, get the permissible stresses 
        for fatigue in case of ratio k ≤ 0 and k > 0 for tension 
        and compression.

        Parameters
        ----------
        df      : pandas DataFrame ; data for the calculation of 
                                     the stresses for fatigue.
        sigma_E : int              ; [MPa] elastic limit of steel.
        sigma_R : int              ; [MPa] ultimate tensile 
                                     strength of steel.
        """
        
        DataFrame.__init__(self, df)
        
        self.sigma_W = self.get_sigma_W()
        self.sigma_E = sigma_E
        self.sigma_R = sigma_R

Los metodos para obtener las diferentes fórmulas son los siguientes:

• Caso de \(\kappa\) igual o menor de 0 (negativo) y tensión de tracción.

  Como se ha indicado arriba, la expresión que define la tensión de tracción es:

  \[\kappa \leq 0 \text{ para tracción: } \sigma_t = \sigma_W · \frac{5}{3 – 2 · \kappa} \leq 0,66 · \sigma_E\]

    def tension_stress_k_neg(self, k):
        """
        Permissible stress for k ≤ 0 and tension.
        
        Parameters
        ----------
        k : pandas Serie ; ratio between the extreme stresses.
        """
        
        sigma_t = self.sigma_W * 5 / (3 - 2 * k)
        sigma_t = sigma_t.where(
            sigma_t <= 0.66 * self.sigma_E, 0.66 * self.sigma_E
            )
        
        return sigma_t

• Caso de \(\kappa\) igual o menor de 0 (negativo) y tensión de compresión.

  \[\kappa \leq 0 \text{ para compresión: } \sigma_c = \sigma_W · \frac{2}{1 - \kappa}\]

    def compression_stress_k_neg(self, k):
        """
        Permissible stress for k ≤ 0 and compression.
        
        Parameters
        ----------
        k : pandas Serie ; ratio between the extreme stresses.
        """
        
        sigma_c = self.sigma_W * 2 / (1 - k)
        
        return sigma_c

• Caso de \(\kappa\) mayor de 0 y tensión de tracción:

  \[\kappa > 0 \text{ para tracción: } \sigma_t = \frac{\sigma_O}{1 - \left(1 - \dfrac{\sigma_O}{\sigma_{+1}}\right) · \kappa} \leq 0,66 · \sigma_E\]

  Además \(\sigma_0\) = tensión de tracción para \(\kappa\) = 0 se da en la fórmula (1), esto es: \(\sigma_0 = 1,66 · \sigma_W\).

  Y \(\sigma_{+1}\) = tensión de tracción para \(\kappa\) = +1, esto es, la tensión última \(\sigma_R\) dividida por el coeficiente de seguridad 1,33: \(\sigma_{+1} = 0,75 · \sigma_R\).

    def tension_stress_k_pos(self, k):
        """
        Permissible stress for k > 0 and tension.
        
        Parameters
        ----------
        k : pandas Serie , ratio between the extreme stresses.
        """
        
        sigma_0 = self.tensile_stress_k_0()
        sigma_1 = self.tensile_stress_k_1()
        sigma_t = sigma_0 / (1 - (1 - sigma_0 / sigma_1) * k)
        sigma_t = sigma_t.where(
            sigma_t <= 0.66 * self.sigma_E,  0.66 * self.sigma_E
            )
        
        return sigma_t

Las tensiones \(\sigma_0\) y \(\sigma_{+1}\) están definidas en los siguientes métodos de la clase:

    def tensile_stress_k_0(self):
        """Tensile stress for k = 0."""
        
        sigma_0 = 1.66 * self.sigma_W
        
        return sigma_0
    
    def tensile_stress_k_1(self):
        """Tensile stress for k = +1."""
        
        sigma_1 = 0.75 * self.sigma_R
        
        return sigma_1

• Caso de \(\kappa\) mayor de 0 y tensión de compresión:

  \[\kappa > 0 \text{ para compresión: } \sigma_c = 1,2 · \sigma_t\]

    def compression_stress_k_pos(self, k):
        """
        Permissible stress for k > 0 and compression.
        
        Parameters
        ----------
        k : pandas Serie : ratio between the extreme stresses.
        """
        
        sigma_t = self.tension_stress_k_pos(k)
        sigma_c = 1.2 * sigma_t
        
        return sigma_c

La tercera clase PermissibleSigma hereda de la clase Formulae los diferentes atributos y métodos. Aquí obtengo los resultados finales de cada tensión admisible a tracción y compresión en función de si \(\kappa\) toma un valor positivo o negativo.

class PermissibleSigma(Formulae):
    """
    Permissible stresses for fatigue with tensile and comprensive 
    loads according to FEM 2131/2132.
    """
    
    def __init__(self, df, sigma_E, sigma_R):
        """
        Asumes df, sigma_E, sigma_R the data for the calculation of 
        the stresses for fatigue, get the permissible stresses for 
        fatigue in case of ratio k ≤ 0 and k > 0 for tension and 
        compression.

        Parameters
        ----------
        df      : pandas DataFrame ; data for the calculation of 
                                     the stresses for fatigue.
        sigma_E : int              ; [MPa] elastic limit of steel.
        sigma_R : int              ; [MPa] ultimate tensile 
                                     strength of steel.
        """
        
        Formulae.__init__(self, df, sigma_E, sigma_R)
        
        self.k_sx = self.get_k_sx()
        self.k_sy = self.get_k_sy()

Los siguientes métodos definen las tensiones a tracción y compresión.

    def tension_stress(self, k):
        """Permissible stress for tension."""
        
        tension_stress_k_neg = self.tension_stress_k_neg(k)
        tension_stress_k_pos = self.tension_stress_k_pos(k)
        tension_stress = tension_stress_k_neg.where(
            k <= 0, tension_stress_k_pos
            )
        
        return tension_stress
    
    def compression_stress(self, k):
        """Permissible stress for compression."""
        
        compression_stress_k_neg = self.compression_stress_k_neg(k)
        compression_stress_k_pos = self.compression_stress_k_pos(k)
        compression_stress = compression_stress_k_neg.where(
            k <= 0, compression_stress_k_pos
            )
        
        return compression_stress * (-1)  # Compression: (-)

y para finalizar, las tensiones en las diferentes direcciones \(x\) e \(y\).

    def tension_stress_x(self):
        """Permissible stress_x for tension."""
        
        return self.tension_stress(self.k_sx)
    
    def tension_stress_y(self):
        """Permissible stress_y for tension."""
        
        return self.tension_stress(self.k_sy)
    
    def compression_stress_x(self):
        """Permissible stress_x for compression."""
        
        return self.compression_stress(self.k_sx)
    
    def compression_stress_y(self):
        """Permissible stress_y for compression."""
        
        return self.compression_stress(self.k_sy)

Definidas las clases para obtener las tensiones admisibles creo la instancia de la clase para obtener los resultados.

permissible_stress = PermissibleSigma(df, sigma_E, sigma_R)
tension_stress_x = permissible_stress.tension_stress_x()
compression_stress_x = permissible_stress.compression_stress_x()
tension_stress_y = permissible_stress.tension_stress_y()
compression_stress_y = permissible_stress.compression_stress_y()
df['sigma_tx_[MPa]'] = round(tension_stress_x, 1)
df['sigma_cx_[MPa]'] = round(compression_stress_x,  1)
df['sigma_ty_[MPa]'] = round(tension_stress_y, 1)
df['sigma_cy_[MPa]'] = round(compression_stress_y, 1)
cols = [
    'component_group', 'notch_effect', 'sigma_tx_[MPa]', 
    'sigma_cx_[MPa]', 'sigma_ty_[MPa]', 'sigma_cy_[MPa]'
    ]
df[cols]

	component_group	notch_effect	sigma_tx_[MPa]	sigma_cx_[MPa]	sigma_ty_[MPa]	sigma_cy_[MPa]
0	E8	K3	117.0	-140.4	75.0	-90.0
1	E8	K3	109.6	-131.6	124.2	-149.0
2	E7	K4	35.1	-35.6	55.5	-66.6
3	E6	K4	204.1	-244.9	55.9	-61.5
4	E7	K2	94.6	-100.1	110.9	-124.2
5	E8	K4	95.8	-114.9	45.0	-54.0
6	E8	K4	30.7	-31.8	36.8	-40.5
7	E8	K4	47.3	-56.7	150.6	-180.7
8	E6	K0	137.7	-140.5	167.8	-182.1
9	E6	K4	234.3	-281.2	68.3	-82.0

¡Estupendo! Ya tengo los datos de las tensiones admisibles, pero ¿son correctos estos datos? Las clases creadas son una herramienta muy potente que me ahorrará mucho tiempo en futuras comprobaciones, pero al definirlas he podido cometer algún error. Una buena práctica es verificar los resultados con una comprobación paralela e independiente, por ejemplo, con Excel o Smath Sutdio.

Para validar los resultados voy a hacer un cálculo manual de las tensiones \(\sigma_x\) de la barra 1 con el índice 0 del DataFrame.

Grado de acero: S 355

Límite elástico \(\sigma_E = 355 \text{ N/mm²}\)

Tensión de rotura \(\sigma_R = 490 \text{ N/mm²}\)

Grupo de la compnente: E8

Efecto de entalladura: K3

Tensión máxima en la dirección \(x\) \(\sigma_{x,max} = -130 \text{ N/mm²}\)

Tensión mínima en la dirección \(x\) \(\sigma_{x,min} = -59 \text{ N/mm²}\)

(Recordad que las tensiones máxima y mínima se definen en términos de valores absolutos).

\[\kappa = \frac{-59}{-130} = 0,454 > 0\]

Tensión básica según tabla T3-4.5.1.1 \(\sigma_W = 45,0 \text{ N/mm²}\)

\[\sigma_0 = 1,66 \cdot\ \sigma_W = 1,66 \cdot 45,0 = 74,7 \text{ N/mm²}\] \[\sigma_{+1} = 0,75 \cdot\ \sigma_R = 0,75 \cdot 490 = 367,5 \text{ N/mm²}\] \[\sigma_t = \frac{\sigma_0}{1 - \left(1 - \dfrac{\sigma_0}{\sigma_{+1}}\right) · \kappa} =\frac{74,7}{1 - \left(1 - \dfrac{74,7}{367,5}\right) \cdot 0,454} =\] \[= 117,03 \text{ N/mm²} \leq 0,66 · \sigma_E = 0,66 · 355 = 234,3 \text{ N/mm²}\] \[\sigma_c = 1,2 · \sigma_t = 1,2 · 117,03 = 140,44 \text{ N/mm²}\]

Al ser \(\sigma_c\) una tensión de compresión toma el valor negativo: \(\sigma_c = -140,44 \text{ N/mm²}\)

Los valores \(\sigma_t = 117,03 \text{ N/mm²}\) y \(\sigma_c = -140,44 \text{ N/mm²}\) coinciden con los valores sigma_tx_[MPa] y sigma_cx_[MPa] del índice 0 del DataFrame dfcon los resultados. Si no coincidieran, o bien el código sería erróneo (tendría un bug), o bien el error estaría en la verificación.

He hecho la verificación para un caso donde \(\kappa\) es positivo. Para completar la verificación voy a comprobar un caso donde \(\kappa\) sea negativo

La fila con el índice 2 con la barra 3 tiene un \(\kappa\) igual a -0,873.

Grupo de la compnente: E7

Efecto de entalladura: K4

Tensión máxima en la dirección \(x\) \(\sigma_{x,max} = -79 \text{ N/mm²}\)

Tensión mínima en la dirección \(x\) \(\sigma_{x,min} = 69 \text{ N/mm²}\)

\[\kappa = \frac{69}{-79} = -0,873 < 0\]

Tensión básica según tabla T3-4.5.1.1 \(\sigma_W = 33,3 \text{ N/mm²}\)

\[\sigma_t = \sigma_W · \frac{5}{3 – 2 · \kappa} = 33,3 · \frac{5}{3 - 2 · (-0,873)} =\] \[= 35,08 \text{ N/mm²} \leq 0,66 · \sigma_E = 0,66 · 355 = 234,3 \text{ N/mm²}\] \[\sigma_c = \sigma_W · \frac{2}{1 – \kappa} = 33,3 · \frac{2}{1 - (-0,873)} = 35,56 \text{ N/mm²}\]

Al ser \(\sigma_c\) una tensión de compresión toma el valor negativo: \(\sigma_c = -35,56 \text{ N/mm²}\)

Los valores \(\sigma_t = 35,08 N\text{ N/mm²}\) y \(\sigma_c = -35,56 \text{ N/mm²}\) coinciden en este caso también con los valores sigma_tx_[MPa] y sigma_cx_[MPa] del índice 2 del DataFrame df con los resultados.

El siguiente paso será calcular las tensiones admisibles para la tensión de cortadura.